↓Skip to main content
Eliezer de Souza da Silva

Eliezer de Souza da Silva

Researcher in Probabilistic AI/ML, Statistics and Data Science

Recent

Paper Accepted at ICLR 2025 (Spotlight): When do GFlowNets Learn the Right Distribution?

·256 words
Blog News Paper Accepted
I am delighted to announce that our paper, When do GFlowNets Learn the Right Distribution?, has been accepted for presentation at ICLR 2025! This work advances our theoretical understanding of Generative Flow Networks (GFlowNets) by examining the impact of balance violations on their ability to approximate target distributions and proposing a novel metric for assessing correctness.

When do GFlowNets Learn the Right Distribution?

·274 words
Tiago Da Silva Rodrigo Barreto Alves Eliezer De Souza Da Silva Amauri H Souza Vikas Garg Samuel Kaski Diego Mesquita Publication Spotlight Paper Conference ICLR Generative Flow Networks Generative Models Theoretical Machine Learning

Analysis of the limitations and stability of GFlowNets under balance violations, showing how these affect accuracy. We introduce a novel metric for assessing correctness, improving evaluation beyond existing protocols.

ICLR 2025 (Spotlight, ~top 5% 🎉)

On Divergence Measures for Training GFlowNets

·277 words
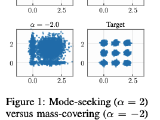
Tiago Da Silva Eliezer De Souza Da Silva Diego Mesquita Publication Conference NeurIPS Deep Generative Models Statistical Divergences Variational Inference Generative Flow Networks

Novel approach to training Generative Flow Networks (GFlowNets) by minimizing divergence measures such as Renyi-$\alpha$, Tsallis-$\alpha$, and Kullback-Leibler (KL) divergences. Stochastic gradient estimators using variance reduction techniques leads to faster and stabler training.

NeurIPS 2024 (Poster)